Dynamic modulation vs. static retuning techniques - part two
Dynamic Modulation “enables you to instantly change the anchor settings of your scale, to move the note that the tonic note of the scale appears on to a new anchor key, and to transpose the anchor frequency of the scale accordingly so that things line up.” (from the LMSO manual)
This short movie shows what happens when Dynamic Modulation is enabled on LMSO.
The scale used for this example is GammaTetra7 shown in Part 1 of this article.
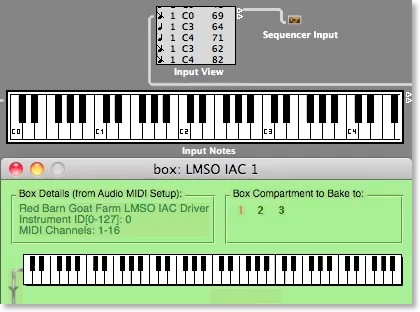

(click on the image to watch the movie)
Keys from C0 to F#0 have been assigned to control modulation.
Same keys on the keyboard play different intervals depending on the selected anchor key:
In C, keys C3/C4 play a 1193.3 cents interval
In D#, keys C3/C4 play a 1228.4 cents interval
In D#, keys C3/F3 play a 526.5 cents interval
In C, keys C3/F3 play a 491.4 cents interval
In C, keys C3/Eb play a 281.3 cents interval (20:17 ratio)
In D#, keys C3/Eb play a 315.6 cents interval (6:5 ratio)
Explanation:
Our “GammaTetra7” scale has 2 kinds of steps: 6 large ones at 105.293 cents each and 1 small one at 70.195 cents.
Let’s call the large steps “L” and the small ones “s”.
What’s going to happen when we move the “anchor key” from one note of the scale to another one? This diagram shows what happens:


The 7 rows indicate the 7 possible anchor keys and the 20 columns indicate the 20 possible steps of Carlos Gamma tuning system.
(1’s indicate a note on that step)
Starting with C we get a “L L L s L L L” scale, starting with C# we get a “L L s L L L L” scale and so on.
After the 7 possible rotations we have touched 13 of the 20 possible steps of Carlos Gamma (of course we can not have more than 7 available steps at a time).
Another diagram shows the results:
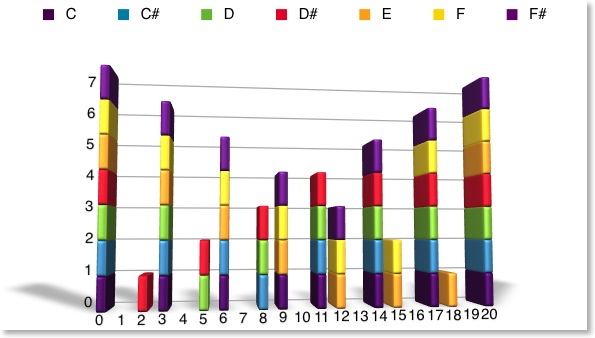

You can see which steps are used and how often they appear, depending on the “anchor key”. You can notice the symmetry of patterns.
It is like if we had built the above mentioned linear scale (shown in Part 1 of this article) building a chain of 13 generating intervals (instead of 7).


This scale uses the following Gamma steps: 0, 2, 3, 5, 6, 8, 9, 11, 12, 14, 15, 17, 18, 20 (the difference among steps is 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2, 1, 2 Gamma steps, making it, again, a MOS scale).
Dynamic Modulation allows us to accommodate 13 pitches within a 7 steps user interface.
Listen to Namul2, a short song using this technique.
Is this a useful technique?
As Jeff Scott privately told me: “dynamic modulation is more dramatic with JI and other more irregular scales” (than MOS scales)
I posted a couple of examples of “dramatic dynamic modulation” on YouTube: Piano11 and CarlosGlass1
Both pieces use forms of JI and you can easily hear something “unusual” going on!
For more explanations click CarlosGlass1 and/or Piano11.
One last consideration:
Setting up a system capable of “dynamic modulation” (shown here) is much trickier than setting up a system for “static retuning techniques” (shown in Part 1).
Look at this picture:

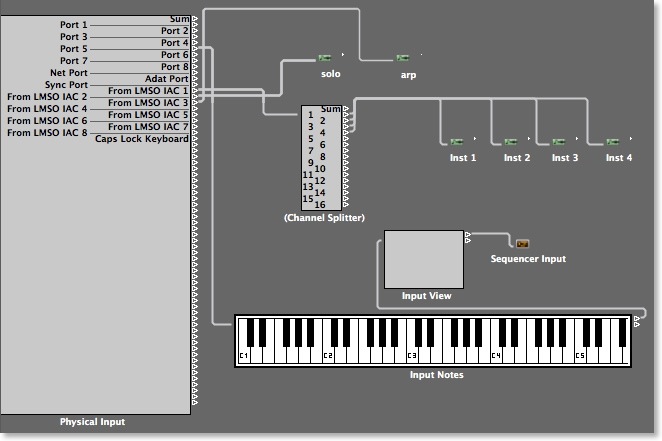
It shows Logic Pro’s Environment page for the song Namul2.
Midi data from the master keyboard (port 5 of midi interface) go to Logic’s input. From there to LMSO to be retuned and “dynamically modulated” and back to Logic through IAC (Inter Application Communication protocol).
You see I use 3 IAC (Inter Application Communication protocol) ports:
LMSO IAC 1 is connected to a channel splitter sending data to 4 monophonic instances of Camel Audio Alchemy playing 4 different “pad” sounds.
LMSO IAC 2 is connected to a monophonic instance of Spectrasonics Omnisphere playing a guitar sound.
LMSO IAC 3 is connected to another monophonic instance of Camel Audio Alchemy playing an arpeggiated sound.
So, I would go through all these complications only for good reasons!
It does not mean I endorse static retuning techniques, I am simply saying that they are simpler to implement and good enough for many situations.


