Modes of Beta
08 May 2011 Filed in: Tuning
Theory
Every once in a while I wonder about how to use my Halberstadt keyboard (HK) for xenharmonic music. Now it’s the time to adapt Carlos Beta to it.
Carlos Beta divides the interval 3:2 into 11 equal steps whereas 12tET (for which HKs are built) divides the same interval into 7 steps, so, the first approach was to choose 7 out of 11 Beta steps to fit the usual “Western” note layout of a perfect fifth.
After a few experiments I arrived to the following rules for selecting notes: only 2 step sizes are allowed where the large one is twice the small one (L = 2s) and adjacent small steps are to be avoided. Doing so, the resulting scale is more evenly distributed and closer to the chromatic “Western” one (of course, if other results are desirable different choices can be made).
The chromatic mode I have created uses the following Beta steps: 0, 2, 3, 5, 6, 8, 10, 11 (L, s, L, s L, L, s) that results in the following scale 0, 127.628, 191.442, 319.07, 382.885, 510.513, 638.141, 701.955 cents (other modes can be created rotating these intervals). I named this scale Carlos Beta PIANO1.

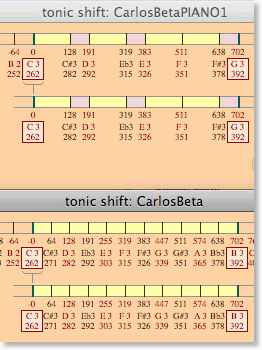
On the above picture you can compare Carlos Beta’s note layout with that of Carlos Beta PIANO1.
Other scales I tried but discarded early on, because not compliant with the above stated rules, were: s, L, s, s, L, L, L (2 adjacent small steps) and s, s, s, L, L, L, L (3 adjacent small steps).
Seasoned microtonalists can easily see that the scale I built is quite consonant (having very good thirds) but it remains a non-octave scale with all its quirkiness if used for tonal music.
Because of the uneven distribution of pitches, pseudo-octaves can be either 1212.5 or 1148.7 cents, major thirds 382.9 or 446.7 cents, minor thirds 319.1 or 255.3 cents and so on.
Not only that, the same interval may sound different on distinct areas of a HK, so, for example, if the interval C3-E3 measures 382.9 cents C2-E2 is 446.7 cents wide because of the non-octave nature of the scale. For these reasons the scale is quite untamable.
Another approach I tried, trying to fit Carlos Beta to the constraint of a HK, was to consider it the 19 equal division of a stretched octave 1212.468 cents wide (see 19edo vs. Carlos Beta).
So, instead of choosing 7 out of 11 Beta steps I selected 12 out of 19 of them. Extending the Carlos Beta PIANO1 pattern I arrived to the following “chromatic” scale:

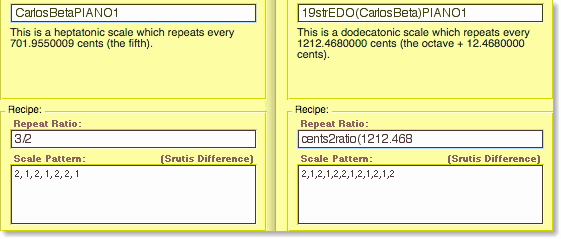
This scale is more “tamable” because it repeats every 12 steps but still has its “wolf” intervals: 1 out of 12 “perfect fifths”, for example, is 765.8 cents wide!

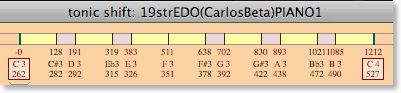
You may like the higher predictability of this second scale depending on the material to be played.
I tried alternating the 2 scales with LMSO, changing the MIDI channel of my HK:

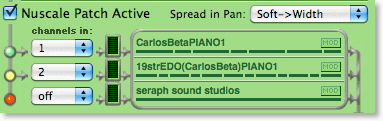
I also tried alternating between Carlos Beta, on my Chameleon and these modes on my HK:

My conclusion is that (paraphrasing Joseph Yasser) the highway of tonal evolution will proceed from new tuning systems and consequent user interfaces (such as isomorphic keyboards) but there can be “byways” in the form of modes of new tuning systems, like the ones examined here, that can be played on established user interfaces, like HKs, that may be useful for those already acquainted with them.
Listen to tiBETAn Dreams, an audio example of Carlos Beta PIANO1 played on a HK.


