KYMI Exercise #1
KNOWING YOUR MUSICAL INTERFACE (KYMI) EXERCISE #1

Click on the picture to watch the movie
This is intended as an example of technical exercise to familiarize with a new musical interface and/or tuning system. The idea is to adapt existing exercises and techniques, written for different musical instruments and tuning systems, to alternative setups (this is the exercise I was referring to in my previous article).
This exercise presents the same 8 bars pattern repeated 4 times.
The pattern looks simple and would sound something like this (if it were in 12tET):


But because it is in Carlos Gamma and because it gets transposed 1 Carlos Gamma Step (CGS) up (35.1 cents) each time, it is quite tricky to play. In order to show the 4 patterns, I have used different colors for the following diagram:

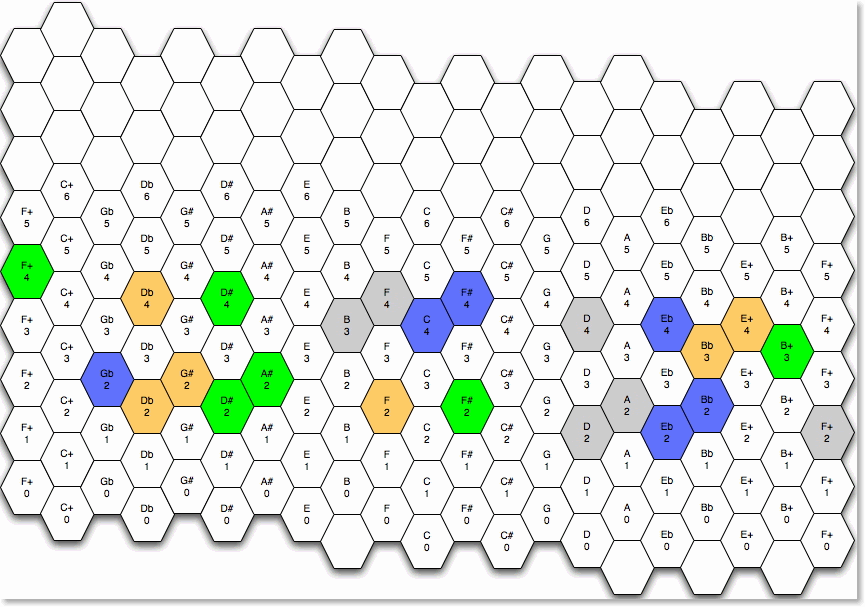
Below you find the order of notes I played, trying to explain the relationship among them so, for example, I start with G#2 (in parentheses you see the pitch relationship with the root note of the arpeggiator) then I play E+4 (34 CGS above G#2) and so on.
All note names refer to my “C central” note layout.
You can see the first 8 bars in Gamma notation here.
YELLOW PATTERN (arpeggiator’s root note: C1)
G#2 (C1+34 CGS) > E+4 (G#2 + 34 CGS) > G#2
F2 (C1 + 29 CGS) > Db4 (F2 + 34 CGS) > F2
Db2 (C1 + 23 CGS) > Bb3 (Db2 + 34 CGS) > Db2
F2 (C1 + 29 CGS) > Db4 (F2 + 34 CGS) > F2
34 CGS = 1193.3 cents
29 CGS = 1017.8 cents
23 CGS = 807.2 cents
GRAY PATTERN (arpeggiator’s root note: C+1)
same as previous one but starting on
A2 (G#2 + 1 CGS)
GREEN PATTERN (arpeggiator’s root note: C#1)
same as previous one but starting on
A#2 (A2 + 1 CGS)
BLUE PATTERN (arpeggiator’s root note: Db1)
same as previous one but starting on
Bb2 (A#2 + 1 CGS)
FINALE (arpeggiator’s root note: C1)
G#2 (C1+34 CGS) > E+4 (G#2 + 34 CGS) > C#6 (E+4 + 34 CGS) > C1
Looking at the above diagram you can see that the orange and blue patterns span 16 columns, the gray one 13 columns and the green one 20 columns and all of them, regardless of their span, have different shapes.
This is because, for a huge tuning system like Carlos Gamma, it would take a much larger isomorphic keyboard to accommodate all the possible permutations of even a simple line like the one presented here.
Link:
http://matrixsynth.blogspot.com/2010/11/kymi-exercise-1.html


