Dynamic modulation vs. static retuning techniques - part one
24 March 2010 Filed in: Music | Tuning
Theory
This is the first installment of a two-part article about “dynamic modulation vs. static retuning techniques”
Lately I have been thinking of ways to nicely accomodate Carlos Gamma tuning system to an Halberstadt keyboard.
The only way is to find modes that somehow fit its note layout.
One mode that seems to be reasonable is the one I call “GammaTetra7” using 7 out of 20 Gamma steps so that 3:2 (Gamma’s repeat ratio) fits into 7 keys of a regular keyboard (from C to F#, for example), making it very similar to 12tET.
How to create such a mode:
This mode is a classic example of a linear scale: a chain of one interval (generator) divided down into another interval (repeat ratio).
In this case the generator interval is 105.293 cents (3 Gamma steps or 3:2^3:20) and the repeat ratio is 3:2.
(1 Gamma step equals 35.097 cents)
Creating a chain of 7 such intervals and folding them into the repeat ratio we get a mode using the following Gamma steps:
0, 3, 6, 9, 11, 14, 17, 20 (the difference among steps is 3, 3, 3, 2, 3, 3, 3 Gamma steps, making it a MOS scale)

Listen to Namul1, a short song using this mode.
Depending on the synthesizers at hand, setting up a synth to play such a scale is simply a matter of saving it in the required format and loading it on the synth.
In this case I saved the scale in .TUN format (with LMSO) and loaded it into 3 polyphonic instances of Camel Audio Alchemy.

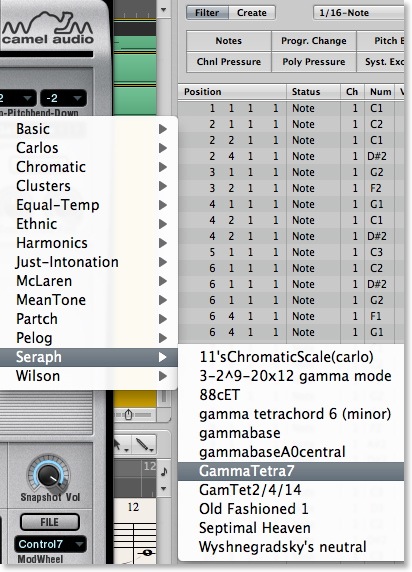
The objection to the use of this mode could be that it sounds too similar to 12tET even though it is still a nonoctave scale, so, why bother?
I have an ace up my sleeve to spice things up a bit called “dynamic modulation”...
Wait for Part 2 of this article.


