The Spiral of Fifths
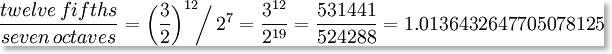
I am preparing for an
upcoming lecture, at NYU in Florence, about the
"Evolution of Tuning Systems", so, I am trying to
figure out a way to demonstrate some tuning
techniques in a comprehensible and "entertaining"
manner.
I am convinced nothing beats a good tutorial video
and this is an example introducing the
Pythagorean tuning system
and the,
so called, spiral of fifths.
If the only way to build intervals is stacking
perfect fifths, as in the Pythagorean system, this is
what happens:
A perfect fifth equals
ratio 3/2 and measures
701.955 cents. It is "just" 1.955
cents wider than a
tempered one.
This "micro" interval is below what is generally
considered the threshold of JND (just noticeable
difference) set at around 5 cents, and can be
perceived only under very special circumstances as
a slow "beating" between the 2
frequencies, depending on many different factors
such as timbre, loudness, register and duration.
Many would conclude that such a small interval is not
relevant and unnoticeable but this experiment shows
the opposite because small and "insignificant"
differences quickly add up to major ones such as the
famous "Pythagorean comma".
The circle of fifths, that all music
students are required to learn (maybe), is
"a geometrical
representation of
relationships" among the 12 notes
of equal temperament
system,
but what happens when we try the same with
"just" fifths? Every
consecutive fifth introduces a difference of 1.955
cents and after 12 of them we do not get back to
our starting point (as in equal temperament) but
to a pitch that is 23.46 cents higher than that
(this small interval is called Pythagorean comma)
and clearly noticeable!
This is why we talk about a spiral of fifths,
because, given a starting point (usually called root
or fundamental note), pitches populate a ever
expanding world of notes that get further and further
away from its center (a mind boggling problem that
has fascinated music theorists, musicians and
instrument builders for thousands of years).

(click on the image to watch the movie)
This short video shows what happens:
We start on C and move along the spiral of justly
tuned perfect fifths until we get to B#, that in
equal temperament is enharmonically the same of C but not
here. It is easy to hear the difference between B#
and C (B# is 23.46 cents sharper than C). This
spiral of fifths is repeated twice and ends with
both B# and C sounding together.
I hope you enjoyed it!!
Isn’t this explanation comprehensible and
entertaining?
Let me know!
R. C. commented:
The epic of gilgamesh
is based entirely on the fifth, in fact it is his
name "two thirds"
it applies directly to the zodiac, because Gilgamesh
as a god traverses the cosmos "riding" on the
fifth. He goes for example from Gemini to
Scorpio. In fact he goes anticlockwise, 5
steps, a journey back in time in this context.
By repeated journeys he marks out the square of the
sun festivals, he "squares the
earth".
A. L. commented:
Very good Carlo! Even
I got that. Comprehensible and entertaining it was
![]()


