Tetrachordal Gamma
Listen first to Glorious Guitars, a short piece based on the following theory. For me, experience comes first, then theory follows!
(a new version of Glorious Guitars is featured on my Gammatar album)
Wikipedia defines a tetrachord as “a series of four tones filling in the interval of a perfect fourth, a 4:3 frequency proportion.” It was a cornerstone of ancient Greek music theory.
Traditionally 2 consecutive tetrachords plus a whole tone ( 9:8 ratio) create an octave (4:3 + 9:8 + 4:3 = 2).
In 12tET terms it is something like these chains of intervals:
C - F, F - G, G - C or
C - F, F - Bb, Bb - C
Gamma stands for Carlos Gamma, the tuning system devised by Wendy Carlos dividing a perfect fifth (ratio 3:2) into 20 equal steps.
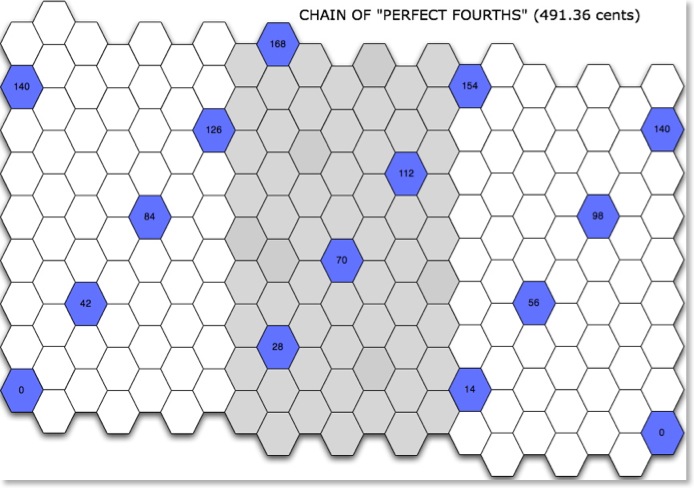
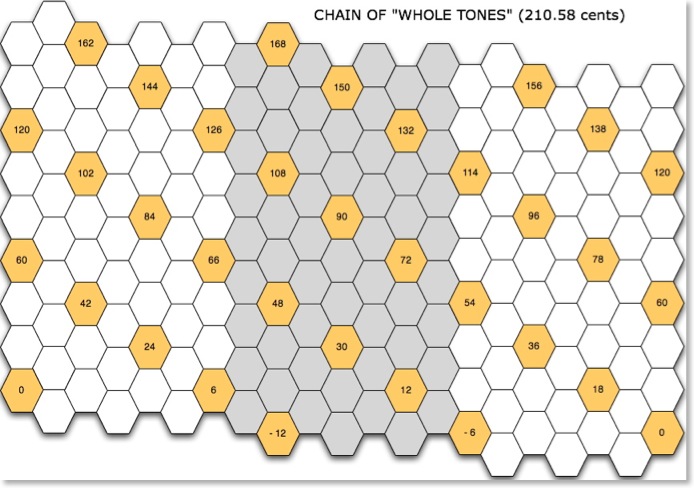
While studying Carlos Gamma on my Opal Chameleon I noticed patterns of perfect fourths and whole tones that reminded me of tetrachords. Gamma has good approximations of both intervals: 491.36 cents (instead of 498.04) for the perfect fourth and 210.58 cents (instead of 203.91) for the whole tone.
A step in Carlos Gamma measures 35.09 cents. So, a pseudo perfect fourth equals 14 steps and a pseudo whole tone equals 6 steps.
The following diagrams use the note layout I introduced with my previous piece “Gamma Elegy”:
Combining and modifying the two previous patterns I came up with a new visual pattern for my Chameleon:

Blue keys follow the pattern 0, 7, 14, 21 et cetera. Yellow ones 0, 6, 12, 18 et cetera. Keys 42, 84, 126 and 168 appear as blue, but they could also be yellow (those numbers are all multiples of both 6 and 7).
Imagine to create tetrachords, as with octave based tuning systems and from two of those create a 7 steps scale:
Let’s try this one: 0, 6, 9, 14 (a minor tetrachord) then repeat the same a fifth above (20, 26, 29, 34). The two tetrachords are divided by 210.58 cents.
Since going north (using this note layout) we move up a fifth, the 2 tetrachords share the same 4 columns!
Listen to Minor Tetrachord
A major tetrachord could be 0, 6, 11, 14 and the second one 20, 26, 31, 34.
Listen to Major Tetrachord
Imagine how many tetrachords we can come up with with 14 subdivisions of a fourth!!!
The following picture shows both major and minor tetrachords starting on keys 0 and 70. You can see the different location of scale degrees depending on the starting note.

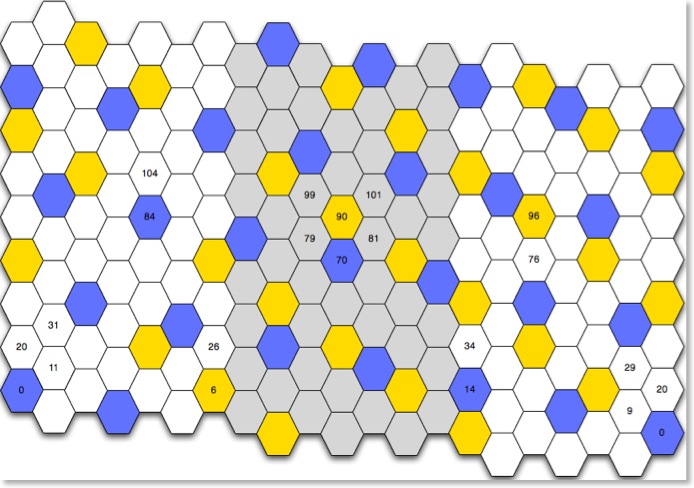
You will have probably noticed by now that the two outermost columns are the same. Gamma divides its framework interval into 20 equal steps, a Chameleon has 21 columns so, after 20 columns we are back to the starting point!
Why try to apply a theory derived from octave based tuning systems to a non octave one? The answer could be that exploring such tuning systems is not easy and I think it is good to start from something we are familiar with, plus, we could create melodic scales that sound familiar and "eerie" at the same time.
So, we have come full circle to the starting point of this article: listen again to Glorious Guitars, enjoy!


